This function creates the samples and evaluates the limit state functions in structural reliability problems. Based on the data, it calculates probabilities of failure and reliability indexes.
results_about_data, failure_prob_list, beta_list = sampling_algorithm_structural_analysis(setup)
Input variables
| Name | Description | Type |
|---|---|---|
setup | Dictionary containing the main configurations. The keys include:
| Dictionary |
Output variables
| Name | Description | Type |
|---|---|---|
results_about_data | Results about reliability analysis | DataFrame |
failure_prob_list | Failure Probability | List |
beta_list | Reliability index | List |
To use the sample algorithm, you must choose the algorithm and variable types and correctly fill in the 'numerical model' and 'variables settings' keys. See the following examples and distributions.
Table 1. Details of 'numerical model' key.
| Type | Sintax |
|---|---|
| Crude Monte Carlo | 'numerical model': {'model sampling': 'mcs'} |
| Latin Hypercube | 'numerical model': {'model sampling': 'lhs'} |
| Stochastic - Crude Monte Carlo. Considering five steps in this example |
|
| Stochastic - Latin Hypercube. Considering five steps in this example |
|
¹When applying a stochastic procedure, use a list in
'none variables'with the same length as'time steps'. We use five steps between 0 and 50 years in this example. In this case, a user should import the Numpy library to usenp. linspace. Another library can be used to create a list.
²When applying a stochastic procedure, you must use the following code on top of the objective function:
id_analysis = int(x[-1])
time_step = none_variable['time analysis']
t_i = time_step[id_analysis]
Table 2. Details of 'variable settings' key.
| Key | Description | Example |
|---|---|---|
'type' | Type of the distribution | 'type': 'normal' |
'parameters' | Parameters of the distribution. See the parameters for each distribution | 'parameters': {'mean': 40.3, 'sigma': 4.64} |
'stochastic variable' | Stochastic process ('True' or 'False'). Use 'True' when you wish apply stochastic process | 'stochastic variable': False |
More details about the reliability method are shown in examples 1 and 2.
Example 1
Consider the simply supported beam show in example 5.1 Nowak and Collins [1]. The beam is subjected to a concentrated live load \(p\) and a uniformly distributed dead load \(w\). Assume \(\boldsymbol{P}\) (concentrated live load), \(\boldsymbol{W}\) (uniformly distributed dead load) and the yield stress, \(\boldsymbol{F_y}\), are random quantities; the length \(l\) and the plastic setion modulus \(z\) are assumed to be precisely know (deterministic). The distribution parameters for \(\boldsymbol{P}, \boldsymbol{W}\) and \(\boldsymbol{F_y}\) are given bellow:
| Variable | Distribution | Mean | Coefficient of Variation (COV) |
|---|---|---|---|
| Yield stress \(\left(\boldsymbol{F_y}\right)\) | Normal | 40.3 | 0.115 |
| Live load \(\left(\boldsymbol{P}\right)\) | Gumbel max. | 10.2 | 0.110 |
| Dead load \(\left(\boldsymbol{W}\right)\) | Log-normal | 0.25 | 0.100 |
The limit state function for beam bending can be expressed as:
| \[ \boldsymbol{R} = 80 \cdot \boldsymbol{F_y} \] | (1) |
| \[ \boldsymbol{S} = 54 \cdot \boldsymbol{P} + 5832 \cdot \boldsymbol{W} \] | (2) |
| \[ \boldsymbol{G} = \boldsymbol{R} - \boldsymbol{S} \begin{cases} \leq 0 & \text{failure}\\ > 0 & \text{safe} \end{cases} \] | (3) |
of_file.py
def nowak_collins_example(x, none_variable):
"""Objective function for the Nowak Collins example (tutorial).
"""
# Random variables
f_y = x[0]
p_load = x[1]
w_load = x[2]
capacity = 80 * f_y
demand = 54 * p_load + 5832 * w_load
# State limit function
constraint = capacity - demand
return [capacity], [demand], [constraint]
your_problem.ipynb
# Libraries
from parepy_toolbox import sampling_algorithm_structural_analysis
from obj_function import nowak_collins_example
# Statement random variables
f = {
'type': 'normal',
'parameters': {'mean': 40.3, 'sigma': 4.64},
'stochastic variable': False,
}
p = {
'type': 'gumbel max',
'parameters': {'mean': 10.2, 'sigma': 1.12},
'stochastic variable': False,
}
w = {
'type': 'lognormal',
'parameters': {'mean': 0.25, 'sigma': 0.025},
'stochastic variable': False,
}
var = [f, p, w]
# PAREpy setup
setup = {
'number of samples': 1000,
'numerical model': {'model sampling': 'mcs'},
'variables settings': var,
'number of state limit functions or constraints': 1,
'none variable': None,
'objective function': nowak_collins_example,
'name simulation': 'nowak_collins_example',
}
# Call algorithm
results, pf, beta = sampling_algorithm_structural_analysis(setup)
Post-processing
This section illustrates how to print, plot, and show these results. Consider Example 1 to show examples of post-processing.
Show results - all samples
What are the columns' names in the results variable of Example 1?
# Show results in notebook file (simply use the DataFrame's variable name in code cell)
results
# or
# Show results in python file (using print function)
print(results)
Output details:
+-----+---------+----------+----------+---------+---------+-----------+-------+
| | X_0 | X_1 | X_2 | R_0 | S_0 | G_0 | I_0 |
+=====+=========+==========+==========+=========+=========+===========+=======+
| 0 | 45.4659 | 9.93797 | 0.25921 | 3637.27 | 2048.36 | 1588.91 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
| 1 | 36.4431 | 10.9928 | 0.258726 | 2915.45 | 2102.5 | 812.949 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
| 2 | 29.8578 | 12.2372 | 0.221577 | 2388.63 | 1953.05 | 435.579 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
...
+-----+---------+----------+----------+---------+---------+-----------+-------+
| 997 | 40.3434 | 9.06056 | 0.189791 | 3227.47 | 1596.13 | 1631.34 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
| 998 | 39.6164 | 11.2624 | 0.255042 | 3169.32 | 2095.57 | 1073.74 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
| 999 | 44.8962 | 9.13833 | 0.257097 | 3591.69 | 1992.86 | 1598.84 | 0 |
+-----+---------+----------+----------+---------+---------+-----------+-------+
X_: Random variables;R_: First return in objective function (User defined);S_: Second return in objective function (User defined);G_: Third return in objective function (User defined). State Limit function;I_: Indicator function (PAREpy generate).
If you use two constraints, the PAREpy output shows two
G_columns, twoR_andS_columns, and twoI_columns. The behavior occurs for more constraints.
This problem presents one state limit function. How do we show columns that results respect a relation \(\boldsymbol{G} \geq 0 \)?
# Libraries
import pandas as pd
# Analysis already realized
sorted_positive = results[results['G_0'] >= 0].sort_values(by='G_0', ascending=True)
# Show results in notebook file (simply use the DataFrame's variable name in code cell)
sorted_positive.head(3)
# or
# Show results in python file (using print function)
print(sorted_positive.head(3))
Output details:
+-----+---------+----------+----------+---------+---------+---------+-------+
| | X_0 | X_1 | X_2 | R_0 | S_0 | G_0 | I_0 |
+=====+=========+==========+==========+=========+=========+=========+=======+
| 598 | 26.5787 | 11.1497 | 0.243887 | 2126.3 | 2024.44 | 101.861 | 0 |
+-----+---------+----------+----------+---------+---------+---------+-------+
| 78 | 30.8042 | 11.6821 | 0.285126 | 2464.34 | 2293.69 | 170.65 | 0 |
+-----+---------+----------+----------+---------+---------+---------+-------+
| 279 | 27.7097 | 9.42611 | 0.261363 | 2216.78 | 2033.28 | 183.498 | 0 |
Plot results - all samples
How do we plot \(\boldsymbol{G}_0\) histogram?
# Libraries
import matplotlib.pyplot as plt
# Plot histogram of G_0
plt.hist(results['G_0'], bins=50, alpha=0.7, color='blue')
plt.xlabel("Constraint Value (G_0)")
plt.ylabel("Frequency")
plt.legend()
plt.show()
Output details:
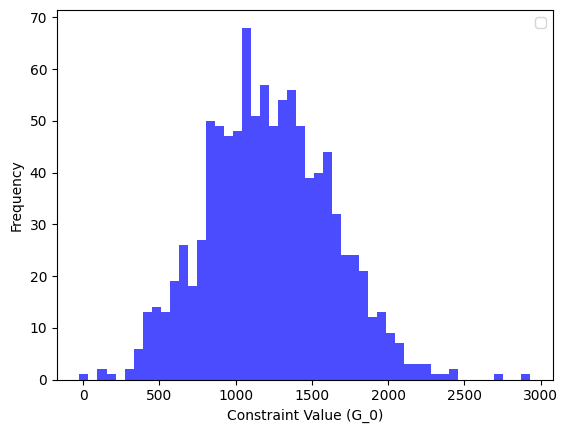
Figure 1. Histogram of \(\boldsymbol{G}_0\).
How do we plot \(\boldsymbol{S}_0\) and \(\boldsymbol{R}_0\) in unique histogram?
# Libraries
import matplotlib.pyplot as plt
# Plot histograms - R_0 and S_0
plt.hist(results['R_0'], bins=50, alpha=0.5, color='green', label='Resistance R_0')
plt.hist(results['S_0'], bins=50, alpha=0.5, color='orange', label='Demand S_0')
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.legend()
plt.show()
Output details:
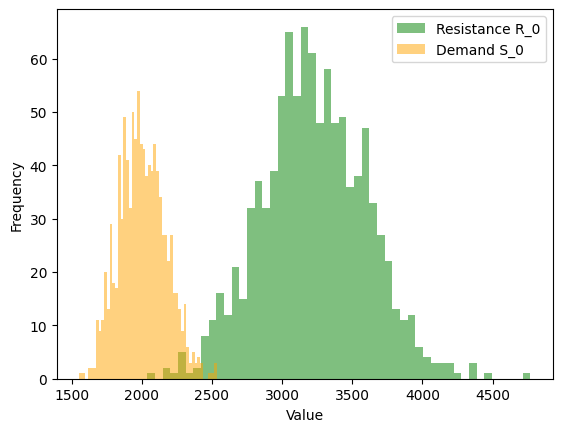
Figure 2. Histogram of \(\boldsymbol{R}_0\) and \(\boldsymbol{S}_0\).
Show \(p_f\) and \(\beta\) results
Show \(p_f\) results in list format.
# Acess pf results
pf_list = pf.values.flatten().tolist()
print(pf_list)
Output details:
[0.0013]
Show \(\beta\) results in list format.
# Acess beta results
beta_list = beta.values.flatten().tolist()
print(beta_list)
Output details:
[3.01145375849978]
How do we print \(p_f\) and \(\beta\) together?
pf_list = pf.values.flatten().tolist()
beta_list = beta.values.flatten().tolist()
for i, (p, b) in enumerate(zip(pf_list, beta_list)):
print(f"State Limite function (g): {i}, pf: {p:.6f}, beta: {b:.6f}")
Output details:
State Limite function (g): 0, pf: 0.003000, beta: 2.747781
State Limite function (g): 1, pf: 0.003000, beta: 2.747781
State Limite function (g): 2, pf: 0.003000, beta: 2.747781
State Limite function (g): 3, pf: 0.004000, beta: 2.652070
State Limite function (g): 4, pf: 0.004000, beta: 2.652070
Example 2
Consider the simply supported beam show in example 5.1 Nowak and Collins [1]. The beam is subjected to a concentrated live load \(p\) and a uniformly distributed dead load \(w\). Assume \(\boldsymbol{P}\) (concentrated live load), \(\boldsymbol{W}\) (uniformly distributed dead load) and the yield stress, \(\boldsymbol{F_y}\), are random quantities; the length \(l\) and the plastic setion modulus \(z\) are assumed to be precisely know (deterministic). The distribution parameters for \(\boldsymbol{P}, \boldsymbol{W}\) and \(\boldsymbol{F_y}\) are given bellow:
| Variable | Distribution | Mean | Coefficient of Variation (COV) |
|---|---|---|---|
| Yield stress \(\left(\boldsymbol{F_y}\right)\) | Normal | 40.3 | 0.115 |
| Live load¹ \(\left(\boldsymbol{P}\right)\) | Gumbel max. | 10.2 | 0.110 |
| Dead load \(\left(\boldsymbol{W}\right)\) | Log-normal | 0.25 | 0.100 |
| ¹Stochastic random variable | |||
The limit state function for beam bending can be expressed as:
| \[ \boldsymbol{R} = 80 \cdot \boldsymbol{F_y} \cdot D\] | (1) |
| \[ \boldsymbol{S} = 54 \cdot \boldsymbol{P} + 5832 \cdot \boldsymbol{W} \] | (2) |
| \[ \boldsymbol{G} = \boldsymbol{R} - \boldsymbol{S} \begin{cases} \leq 0 & \text{failure}\\ > 0 & \text{safe} \end{cases} \] | (3) |
Consider equation (4) for resistance degradation \(\left(D\right)\) [2]. Use 50 years to stochastic analysis (five time steps). Assume that \(P\) load is a stochastic process.
| \[ D(t_i) = 1 - \frac{0.2}{t_i} \cdot 0.01 \] | (4) |
of_file.py
def nowak_collins_time_example(x, none_variable):
"""Objective function for the Nowak example (tutorial).
"""
# User must copy and paste this code in time reliability objective function
###########################################
id_analysis = int(x[-1])
time_step = none_variable['time analysis']
t_i = time_step[id_analysis]
# t_i is a time value from your list of times entered in the 'none variable' key.
###########################################
# Random variables
f_y = x[0]
p_load = x[1]
w_load = x[2]
# Degradation criteria
if t_i == 0:
degrad = 1
else:
degrad = 1 - (0.2 / t_i) * 1E-2
# Capacity and demand
capacity = 80 * f_y * degrad
demand = 54 * p_load + 5832 * w_load
# State limit function
constraint = capacity - demand
return [capacity], [demand], [constraint]
your_problem.ipynb
# Libraries
import pandas as pd
pd.set_option('display.max_columns', None)
import numpy as np
from parepy_toolbox import sampling_algorithm_structural_analysis
from obj_function import nowak_collins_time_example
# Statement random variables
f = {
'type': 'normal',
'parameters': {'mean': 40.3, 'sigma': 4.64},
'stochastic variable': False,
}
p = {
'type': 'gumbel max',
'parameters': {'mean': 10.2, 'sigma': 1.12},
'stochastic variable': True,
}
w = {
'type': 'lognormal',
'parameters': {'mean': 0.25, 'sigma': 0.025},
'stochastic variable': False,
}
var = [f, p, w]
# PAREpy setup
setup = {
'number of samples': 1000,
'numerical model': {'model sampling': 'mcs-time', 'time steps': 5},
'variables settings': var,
'number of state limit functions or constraints': 1,
'none variable': {'time analysis': list(np.linspace(0, 50, num=5, endpoint=True))},
'objective function': nowak_collins_time_example,
'name simulation': 'nowak_collins_time_example',
}
# Call algorithm
results, pf, beta = sampling_algorithm_structural_analysis(setup)
Post-processing
Show results - all samples
What are the columns' names in the results of Example 2?
+-----+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+------------+------------+------------+------------+------------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+
| | X_0_t=0 | X_0_t=1 | X_0_t=2 | X_0_t=3 | X_0_t=4 | X_1_t=0 | X_1_t=1 | X_1_t=2 | X_1_t=3 | X_1_t=4 | X_2_t=0 | X_2_t=1 | X_2_t=2 | X_2_t=3 | X_2_t=4 | STEP_t_0 | STEP_t_1 | STEP_t_2 | STEP_t_3 | STEP_t_4 | R_0_t=0 | R_0_t=1 | R_0_t=2 | R_0_t=3 | R_0_t=4 | S_0_t=0 | S_0_t=1 | S_0_t=2 | S_0_t=3 | S_0_t=4 | G_0_t=0 | G_0_t=1 | G_0_t=2 | G_0_t=3 | G_0_t=4 | I_0_t=0 | I_0_t=1 | I_0_t=2 | I_0_t=3 | I_0_t=4 |
+=====+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+============+============+============+============+============+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+===========+
| 0 | 34.7571 | 34.7571 | 34.7571 | 34.7571 | 34.7571 | 13.5025 | 10.6468 | 10.0188 | 10.3869 | 14.0795 | 0.275001 | 0.275001 | 0.275001 | 0.275001 | 0.275001 | 0 | 1 | 2 | 3 | 4 | 2780.56 | 2780.12 | 2780.34 | 2780.42 | 2780.45 | 2332.94 | 2178.73 | 2144.82 | 2164.7 | 2364.1 | 447.625 | 601.389 | 635.52 | 615.72 | 416.352 | 0 | 0 | 0 | 0 | 0 |
+-----+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+------------+------------+------------+------------+------------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+
| 1 | 40.5636 | 40.5636 | 40.5636 | 40.5636 | 40.5636 | 9.29018 | 9.07671 | 13.0581 | 10.3811 | 10.5524 | 0.276317 | 0.276317 | 0.276317 | 0.276317 | 0.276317 | 0 | 1 | 2 | 3 | 4 | 3245.09 | 3244.57 | 3244.83 | 3244.91 | 3244.96 | 2113.15 | 2101.63 | 2316.62 | 2172.06 | 2181.31 | 1131.93 | 1142.94 | 928.207 | 1072.85 | 1063.64 | 0 | 0 | 0 | 0 | 0 |
+-----+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+------------+------------+------------+------------+------------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+
| 2 | 38.9735 | 38.9735 | 38.9735 | 38.9735 | 38.9735 | 10.6705 | 9.94778 | 11.5999 | 12.1341 | 9.89408 | 0.224981 | 0.224981 | 0.224981 | 0.224981 | 0.224981 | 0 | 1 | 2 | 3 | 4 | 3117.88 | 3117.38 | 3117.63 | 3117.71 | 3117.75 | 1888.29 | 1849.27 | 1938.48 | 1967.33 | 1846.37 | 1229.58 | 1268.11 | 1179.15 | 1150.38 | 1271.38 | 0 | 0 | 0 | 0 | 0 |
+-----+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+------------+------------+------------+------------+------------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+-----------+
X_i_t: Random variables in specific time step;STEP_t_: Time step ID;R_i_t: First return in objective function (User defined) - in specific time step;S_i_t: Second return in objective function (User defined) - in specific time step;G_i_t: Second return in objective function (User defined) - in specific time step;I_i_t: Indicator function (PAREpy generate) - in specific time step.
If you use two constraints, the PAREpy output will show two G_ columns, two R_ and S_ columns, and two I_ columns. However, in time-dependent reliability cases, PAREpy uses first-barrier failure criteria to evaluate the probability of failure. Therefore, all outputs have the same user-specified time interval.
Show \(p_f\) and \(\beta\) results
Show \(p_f\) results in list format. To view results about all time steps in \(G_0\) state limit function folliwing code:
# Acess pf results
pf_list = pf['G_0'].tolist()
print(pf_list)
Output details:
[0.003, 0.003, 0.003, 0.004, 0.004]
Show \(\beta\) results in list format.
# Acess beta results
beta_list = beta['G_0'].tolist()
print(beta_list)
Output details:
[2.7477813854449726, 2.7477813854449726, 2.7477813854449726, 2.652069807902187, 2.652069807902187]
How do we print \(p_f\) and \(\beta\) together?
pf_list = pf['G_0'].tolist()
beta_list = beta['G_0'].tolist()
for i, (p, b) in enumerate(zip(pf_list, beta_list)):
print(f"Time step (id={i}, time={setup['none variable']['time analysis'][i]}), pf: {p:.6f}, beta: {b:.6f}")
Output details:
Time step (id=0, time=0.0), pf: 0.003000, beta: 2.747781
Time step (id=1, time=12.5), pf: 0.003000, beta: 2.747781
Time step (id=2, time=25.0), pf: 0.003000, beta: 2.747781
Time step (id=3, time=37.5), pf: 0.004000, beta: 2.652070
Time step (id=4, time=50.0), pf: 0.004000, beta: 2.652070