This function generates a Lognormal distribution with a specified mean \(\mu\) and standard deviation \(\sigma\).
u = lognormal_sampling(parameters, method, n_samples, seed)
Input variables
| Name | Description | Type |
|---|---|---|
parameters | Dictionary of parameters for the Lognormal distribution. Keys:
| Dictionary |
method | Sampling method. Supports the following values:
| String |
n_samples | Number of samples | Integer |
seed | Seed for random number generation. Use None for a random seed | Integer or None |
Output variables
| Name | Description | Type |
|---|---|---|
u | Random samples | List |
Example 1
In this example, we will use the lognormal_sampling function from the parepy_toolbox to generate two random samples (\(n=400\)) following a Lognormal distribution. The first set is sampled using the Monte Carlo Sampling (MCS) method, and the second using the Latin Hypercube Sampling (LHS) method. The mean and standard deviation are defined as \([1.0, 0.4]\). The results are visualized using histograms with Kernel Density Estimates (KDE) plotted (using matplotlib lib) side-by-side for comparison.
# Library
import matplotlib.pyplot as plt
from parepy_toolbox import lognormal_sampling
# Sampling
n = 400
x = lognormal_sampling({'mean': 1.0, 'sigma': 0.4}, 'mcs', n)
y = lognormal_sampling({'mean': 1.0, 'sigma': 0.4}, 'lhs', n)
# Plot
fig, axes = plt.subplots(1, 2, figsize=(7, 3))
sns.histplot(x, kde=True, bins=30, color='blue', ax=axes[0], alpha=0.6, edgecolor='black')
axes[0].set_title('MCS Sampling')
axes[0].set_xlabel('Values')
axes[0].set_ylabel('Density')
sns.histplot(y, kde=True, bins=30, color='green', ax=axes[1], alpha=0.6, edgecolor='black')
axes[1].set_title('LHS Sampling')
axes[1].set_xlabel('Values')
axes[1].set_ylabel('Density')
plt.tight_layout()
plt.show()
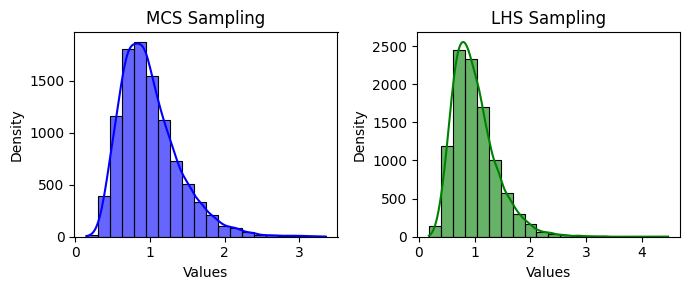
Figure 1. Lognormal variable example.
Example 2
In this example, we will use the lognormal_sampling function from the parepy_toolbox to generate two random samples (\(n=3\)) following a Lognormal distribution. Using the Monte Carlo algorithm and the specific seed (seed=25), we generated 3 times and compared the results.
from parepy_toolbox import lognormal_sampling
# Sampling
n = 3
x0 = lognormal_sampling({'mean': 1.0, 'sigma': 0.4}, 'mcs', n, 25)
x1 = lognormal_sampling({'mean': 1.0, 'sigma': 0.4}, 'mcs', n, 25)
x2 = lognormal_sampling({'mean': 1.0, 'sigma': 0.4}, 'mcs', n, 25)
print(x0, '\n', x1, '\n', x2)
Output details.
[0.6060493388543875, 1.613348026589917, 0.8213467995763253]
[0.6060493388543875, 1.613348026589917, 0.8213467995763253]
[0.6060493388543875, 1.613348026589917, 0.8213467995763253]
Note that using the seed 25 by 3 times, we can generate the same values in a random variable.