Inverse problem
The inverse problem is a form of modelating problems which allow defining the parameters of the analyzed system based on a given data set. For example, it is possible to know the characteristics of a harmonic oscillator system (like the stiffness) just knowing a certain quantity of positions of the mass given through time. Larger data sets mean more accuracy to the value prediction. Taking for example a signal given by a simple equation like:
\[y(t)=acos(bt)\]Taking a=3 and b=4 results in the following graphic:

Now, add some noise to the signal (10%), making it similar to what an experimentally obtained data could be.

In a real case, the equation that produced this graphic would be unknown. Although, it is possible to assume the equation is probally a cosine function due to its form, and so to get back the values of the parameters (in this case, a and b) by using an optimization algorithm, which will optimize the loss function (MSE) that describes how far our prediction is from the real values of the parameters.
\[{OF =\frac{1}{n} \sum^n_{i=0}(y_{pred}^{(i)} - y_{exp}^{(i)})^2}\]Where n is the number of points in the data set, y_{exp} is the y value of the i_th experimentally given point, and y_{pred} is the y value of the i-th given by the equation using the predicted parameters. Basically, the concept is about trying to "guess" which values of wanted parameters can lead to the better aproximation to the results of the experiment. There are several methods to "guess" the parameter values. Solving this example using genetic algorithm, setting a population=50 and 100 max iterations, the following solution appears: a=2.9884694436445205 and b=4.001254870797622, that is a good approximation of the original values of 3 and 4, respectively.
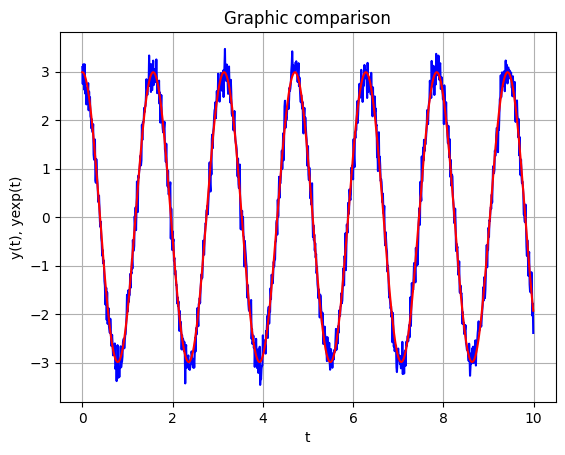
In this application, the optimization technique is used to minimize the deviation between the numerical results and the ones observed experimentally [1], where the Objective Function (OF) is given by equation (1).
| \[ min \left| \mathbf{y}_{\text{true}} - \mathbf{y}_{\text{pred}} \right| \] | (1) |
The section "loss" shows some loss equations implemented in the METApy framework.